Informational Projection Theory (IPT)

A Framework for Emergent Geometry, Entanglement, and Observed Spacetime

Introduction

Informational Projection Theory proposes that the structure of observed reality—including space, time, and causality—emerges from foundational informational relationships. It unifies three conceptual layers: entanglement (Layer 1), emergent geometry (Layer 2), and observer-relative temporal coherence (Layer 3).

The theory is supported by formal theorems, mathematical models, and Python-based entropy simulations.

Bertrand Russell & the Informational Roots of Reality

How does Informational Projection Theory build on early 20th-century logic and metaphysics? Bertrand Russell's concept of logical atoms and structural realism finds new life in IPT's treatment of reality as emerging from entangled information. What Russell could only envision as abstract logic, IPT now simulates and models with physical consequences.

Explore the Russell Connection →

đź“„ Downloadable Paper

Read or download the full IPT paper with mathematical proofs, diagrams, and references.

Download DOCX Download PDF

🧮 Python Tools

Download and run the core simulation tools for testing Informational Projection Theory:

Ensure you have qiskit, matplotlib, networkx, and pandas installed for proper functionality.

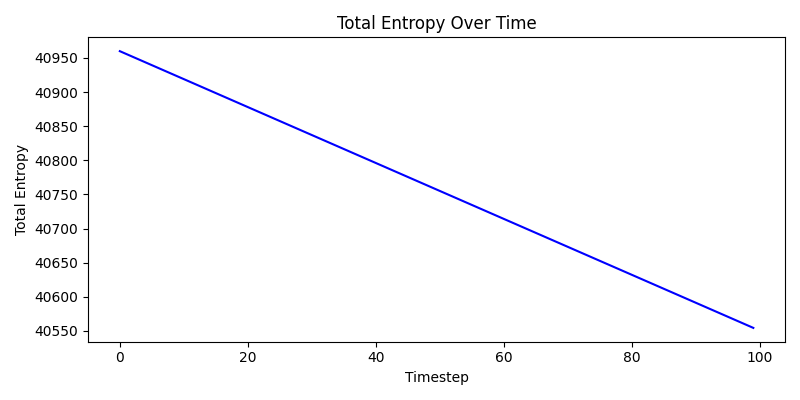
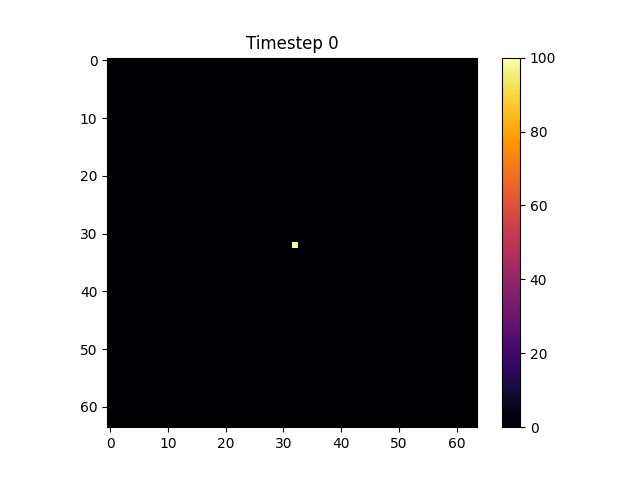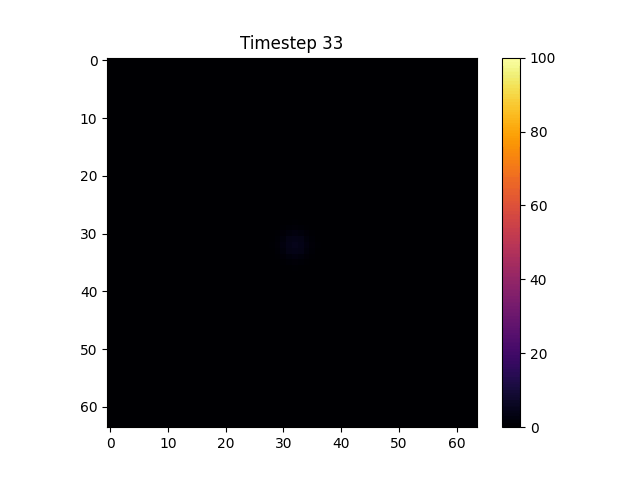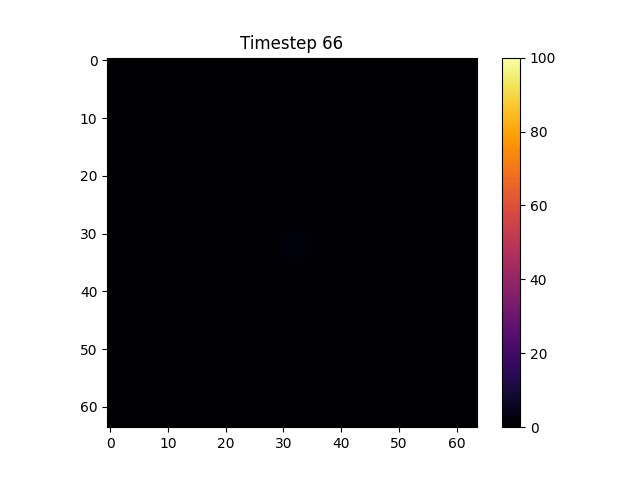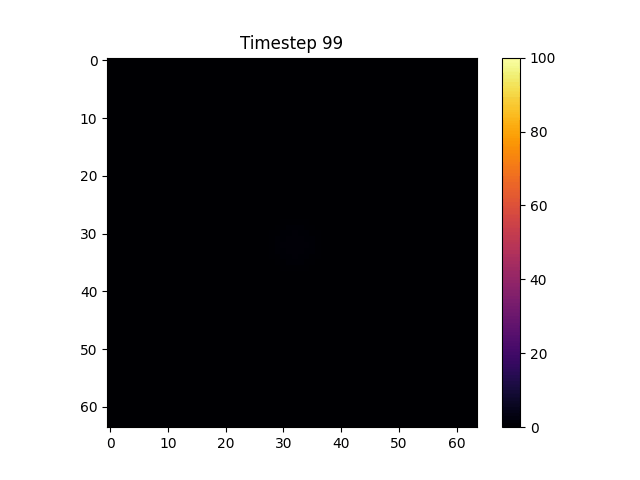
đź“Š Simulated Figures & Results

View animated simulations of entropy evolution and emergent geometry under different configurations.

Global Initialization

Global Initialization GIF
Global Initialization Trend

Local Spike Initialization

Local Spike Initialization GIF
Local Spike Trend

Local Noise Initialization

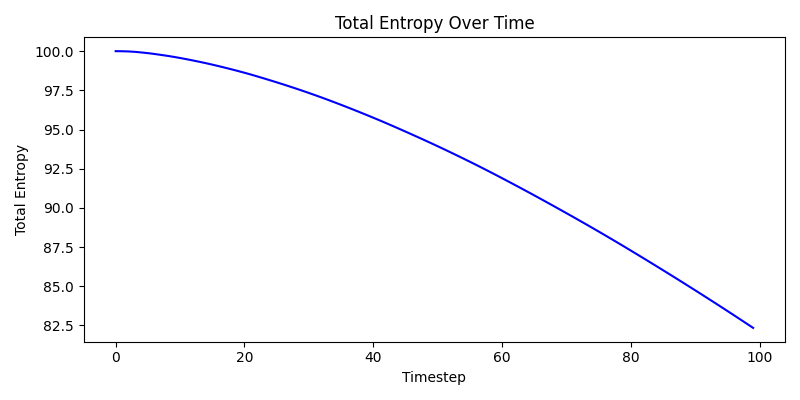
Local Noise Initialization GIF
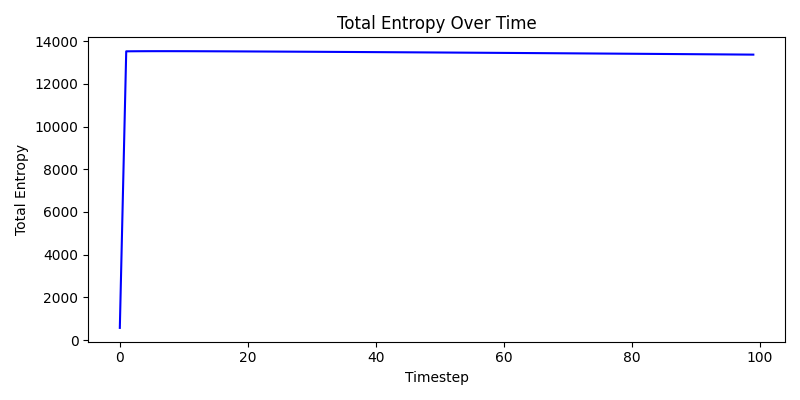
Local Noise Trend

đź“š References & Acknowledgments

Includes foundational influences, academic sources, and contributor credits including AI-assisted formulation.

  1. Bekenstein, J. D. (1973). Black holes and entropy. Physical Review D, 7(8), 2333.
    https://doi.org/10.1103/PhysRevD.7.2333
    ↳ Connects information, entropy, and physical geometry.
  2. Biamonte, J., & Bergholm, V. (2017). Tensor networks in a nutshell. arXiv.
    https://arxiv.org/abs/1708.00006
    ↳ Techniques to represent structured information geometrically.
  3. Cao, C., Carroll, S. M., & Michalakis, S. (2017). Space from Hilbert space. Physical Review D, 95(2), 024031.
    https://doi.org/10.1103/PhysRevD.95.024031
    ↳ Concrete derivation of geometric space from entanglement patterns.
  4. Coifman, R. R., & Lafon, S. (2006). Diffusion maps. Applied and Computational Harmonic Analysis, 21(1), 5–30.
    https://doi.org/10.1016/j.acha.2006.04.006
    ↳ Basis for constructing geometry from local transitions and information diffusion.
  5. Cover, T. M., & Thomas, J. A. (2006). Elements of Information Theory. Wiley-Interscience.
    ↳ Reference for formal information-theoretic concepts used in all three layers.
  6. Donaldson, E. (2025). IPT Python Tools (v1.0) [Python script archive]. Informational Projection Project.
    https://www.informationalprojection.org/downloads/ipt_python_tools.zip
    ↳ Includes supporting code for entropy simulations, MERA structure modeling, and GUI-based projection analysis used in this paper.
  7. Gao, J., Barzel, B., & Barabási, A.-L. (2016). Universal resilience patterns in complex networks. Nature, 530(7590), 307–312.
    https://doi.org/10.1038/nature16948
    ↳ Shows emergence of structural stability and order in complex networks, relevant for Theorem 2.
  8. Gromov, M. (1999). Metric Structures for Riemannian and Non-Riemannian Spaces. Basel: Birkhäuser.
    ↳ Foundation for understanding projection and curvature on informational manifolds.
  9. Petz, D. (2001). Entropy, von Neumann and the von Neumann entropy. Reviews in Mathematical Physics, 15(01), 79–91.
    https://doi.org/10.48550/arXiv.math-ph/0102013
    ↳ Mathematical treatment of entropy in quantum systems.
  10. Ryu, S., & Takayanagi, T. (2006). Holographic derivation of entanglement entropy... Physical Review Letters, 96(18), 181602.
    https://doi.org/10.1103/PhysRevLett.96.181602
    ↳ Key result linking geometry and entanglement.
  11. Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27(3), 379–423.
    https://doi.org/10.1002/j.1538-7305.1948.tb01338.x
    ↳ Foundation of entropy as a measure of information.
  12. Sorkin, R. D. (2003). Causal sets: Discrete gravity (Notes for the Valdivia Summer School). arXiv:gr-qc/0309009.
    https://arxiv.org/abs/gr-qc/0309009
    ↳ Introduction of causal structure and discrete spacetime from an informational basis.
  13. Verlinde, E. (2011). On the origin of gravity and the laws of Newton. Journal of High Energy Physics, 2011(4), 29.
    https://doi.org/10.1007/JHEP04(2011)029
    ↳ Emergent gravity as an entropic force, similar in philosophy to emergent geometry here.
  14. Wheeler, J. A. (1990). Information, physics, quantum: The search for links. In W. H. Zurek (Ed.), Complexity, Entropy and the Physics of Information (pp. 3–28). Addison-Wesley.
    ↳ Conceptual origin of “It from Bit.”

đź’¬ Contact / Feedback

If you have feedback, questions, or would like to contribute, reach out via: